Introduction
In signal processing and RF engineering, filters are fundamental building blocks that shape frequency responses and determine system performance. Whether you’re working on audio processing, communications systems, or embedded hardware, understanding filter topologies is essential for making informed design decisions.
The Butterworth, Chebyshev, Bessel, and Elliptic filters represent the three primary “classical” approximations, each optimized for specific performance characteristics. This article explores these four most common filter types, examining their distinct characteristics that make them suitable for different applications.
Understanding Filter Basics
Before diving into specific filter types, it’s important to understand key concepts:
Passband and Stopband: The passband allows signal frequencies to pass through with minimal attenuation, while the stopband rejects unwanted frequencies. The transition region between these bands is where different filter types show their distinctive characteristics.
Roll-off Rate: This describes how quickly the filter attenuates frequencies in the transition from passband to stopband. It’s typically measured in dB per decade (20 dB/decade = 6 dB/octave per pole).
Filter Order: The order (n) determines the complexity and performance of the filter. A first-order filter has a 20 dB/decade roll-off, second-order has 40 dB/decade, and so on. Higher-order filters provide steeper roll-offs but require more components.
Group Delay: This quantifies the time it takes for a signal to traverse the filter network. Constant group delay within the passband indicates excellent transient response, meaning the input signal is replicated accurately with only a time delay.
The Four Major Filter Topologies
Bessel Filter
Named after German mathematician Friedrich Bessel, the Bessel filter is designed to optimize maximally flat time delay, ensuring constant group delay throughout its passband.
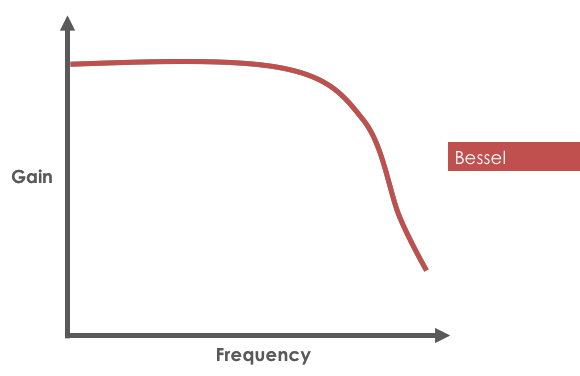 Bessel filter frequency response showing gentle roll-off
Bessel filter frequency response showing gentle roll-off
Key Characteristics:
- Gentlest roll-off among all filter types (slowest transition to stopband)
- Superior phase linearity with minimal phase shift
- Constant group delay resulting in linear phase response
- Excellent step response characteristics without overshoot or ringing
- Requires the most components (stages) to implement
- Low sensitivity to component tolerances
- Monotonically decreasing amplitude response in passband
- Exclusively available with low-pass selectivity
Mathematical Foundation: Bessel filters derive their properties from Bessel polynomials, which prioritize time-domain characteristics over frequency-domain sharpness. The group delay is nearly directly proportional to filter order and inversely proportional to bandwidth.
Best Applications: The Bessel filter excels when maintaining signal timing and shape is critical. In the time domain (transient response), the input signal is replicated exactly with only a delay. This makes them ideal for:
- Pulse transmission systems where signal shape must be preserved
- Video processing where phase distortion affects image quality
- Measurement and instrumentation systems
- Data acquisition systems where signal fidelity matters
- Applications requiring minimal settling time
However, Bessel filters require adequate frequency separation between passband and stopband due to their gradual roll-off. In typical implementations, Bessel filters take the minimum time to settle (around 1ms in standard designs) without any overshoot.
Butterworth Filter
Named after British physicist Stephen Butterworth, who explained its behavior in his 1930 paper “On the Theory of Filter Amplifiers,” this filter is known for its “maximally flat” passband response.
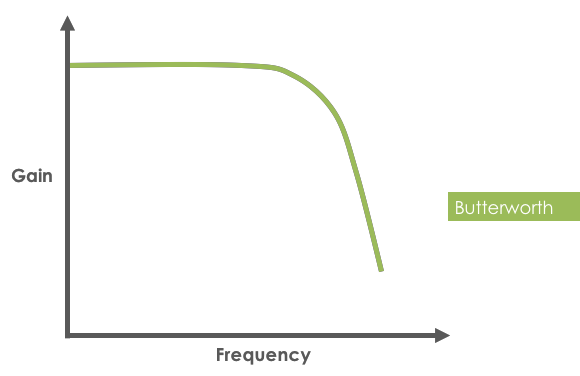 Butterworth filter showing maximally flat passband response
Butterworth filter showing maximally flat passband response
Key Characteristics:
- Flat frequency response in the passband with no ripple (maximally flat magnitude response)
- Monotonic roll-off (smooth and gradual without oscillations)
- Steeper roll-off than Bessel filters
- Moderate phase linearity (better than Chebyshev, worse than Bessel)
- Good balance between selectivity and component count
- Forgiving to component tolerances
- Excellent VSWR (Voltage Standing Wave Ratio) at center frequency
- Poles lie on a circle in the complex plane with equal angular spacing
Roll-off Characteristics: The order of a Butterworth filter directly determines its roll-off rate:
- 1st order: 20 dB/decade (6 dB/octave)
- 2nd order: 40 dB/decade (12 dB/octave)
- 5th order: 100 dB/decade (30 dB/octave)
- nth order: 20n dB/decade
Best Applications: Butterworth filters demonstrate satisfactory amplitude and transient characteristics, making them excellent general-purpose filters. They’re commonly used in:
- Audio applications where flat passband response is critical
- Anti-aliasing filters for ADCs
- Reconstruction filters for DACs
- General signal conditioning where predictable response is needed
- Applications where ripple-free response is valued over maximum selectivity
In standard implementations, Butterworth filters settle in moderate time (around 3ms) with a single 10% overshoot. Their forgiving nature regarding component tolerances makes them popular in practical designs.
Chebyshev Filter
Named after Russian mathematician Pafnuty Chebyshev, these filters achieve faster roll-off by allowing controlled ripple in frequency response.
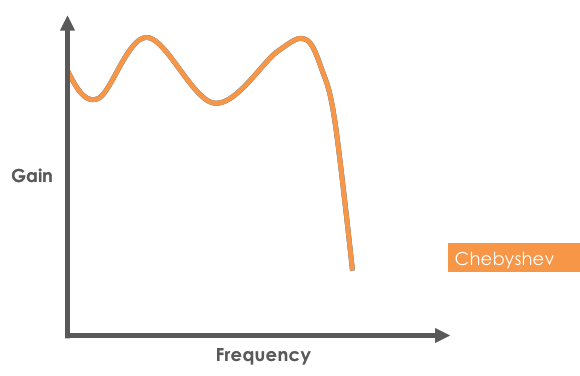 Chebyshev filter showing ripple and steep roll-off
Chebyshev filter showing ripple and steep roll-off
Key Characteristics:
- Steeper roll-off than Butterworth filters of the same order
- Controlled ripple (adjustable design parameter)
- Ripple amplitude is proportional to roll-off steepness
- Relatively non-linear phase response
- Excellent selectivity with fewer components than Butterworth
- Can distort pulses due to non-linear group delay
- Poles lie on an ellipse in the complex plane
- Also known as “equal ripple response” filter
Filter Types:
- Chebyshev Type I: Ripple occurs in the passband, making them suitable for applications emphasizing specific frequency ranges while accepting some ripple
- Chebyshev Type II (Inverse Chebyshev): Ripple occurs in the stopband with maximally flat passband, ideal for minimizing signal distortion in the passband. Used in anti-aliasing and reconstruction filters for converters
Design Trade-off: The gain ripple (measured in dB) is an adjustable parameter. The faster the roll-off desired, the greater the peak-to-peak ripples in the passband. This makes Chebyshev filters highly customizable to application needs.
Phase Response Considerations: The phase response is highly non-linear in the transition region, which can cause severe pulse distortion and increased errors in modern demodulators. The common workaround is increasing the filter bandwidth to push the non-linear phase region further out of the frequency band of interest.
Best Applications: Chebyshev filters enhance amplitude response at the expense of transient behavior. They’re the workhorses of RF and communications systems:
- Channel filtering in communications systems
- Frequency separation where sharp selectivity is paramount
- RF applications where component count must be minimized
- Applications accepting passband ripple for better selectivity
- Situations where steeper roll-off justifies some amplitude variation
In typical implementations, Chebyshev filters take the longest to settle (around 7ms) due to their ringing nature in step response, exhibiting significant overshoot.
Elliptic (Cauer) Filter
Named after German mathematician Wilhelm Cauer, the elliptic filter (also called Cauer, Elliptic-Function, or Elliptic-Integral filter) offers the sharpest possible roll-off by allowing ripple in both passband and stopband.
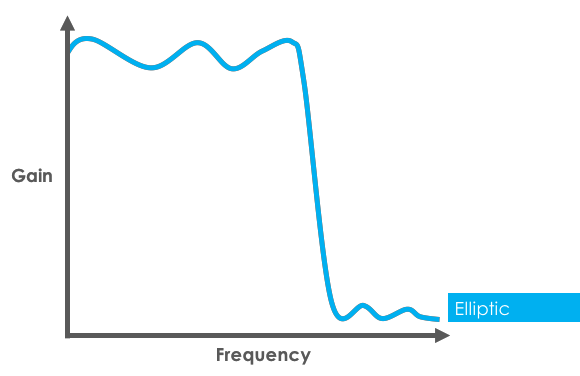 Elliptic filter with ripple in both passband and stopband
Elliptic filter with ripple in both passband and stopband
Key Characteristics:
- Sharpest roll-off of all classical filter types
- Ripple present in both passband and stopband
- Most complex implementation requiring more components
- Independently adjustable passband and stopband ripple
- Superior selectivity compared to all other types
- Highly non-linear phase response
- Includes stopband zeros (loss poles) in the transfer function
- Achieves infinite attenuation at specific frequencies in stopband
Mathematical Relationship: Butterworth and Chebyshev filters are special cases of elliptical filters:
- Zero ripple in both bands → Butterworth filter
- Zero stopband ripple + passband ripple → Chebyshev Type I
- Zero passband ripple + stopband ripple → Chebyshev Type II
- Ripple in both bands → Full Elliptic filter (steepest transition)
Design Flexibility: The elliptic filter’s defining feature is the ability to tune passband and stopband ripple independently. This flexibility allows engineers to optimize the filter precisely for their specifications, trading ripple amplitude for transition steepness.
Best Applications: When frequency selectivity is paramount and you need to squeeze maximum performance from limited frequency space, elliptic filters shine:
- High-performance communications systems with tight channel spacing
- Spectrum analysis equipment requiring maximum adjacent channel rejection
- Applications where both space and frequency spectrum are constrained
- Systems where phase linearity is less critical than frequency selectivity
- Designs prioritizing sharp frequency discrimination over time-domain characteristics
Despite the passband and stopband ripple, elliptic filters’ widespread use stems from providing the sharpest transition between passband and stopband for a given filter order.
Comparative Analysis and Design Trade-offs
When selecting a filter topology, engineers must balance multiple competing factors. Understanding these trade-offs is crucial for optimal design decisions.
Frequency Response vs. Phase Linearity
The fundamental trade-off in filter design exists between frequency selectivity and phase linearity:
- Bessel: Prioritizes linear phase (constant group delay) at the expense of frequency selectivity. Best transient response.
- Butterworth: Balanced compromise with moderate phase linearity and moderate selectivity. Good transient response.
- Chebyshev: Sacrifices phase linearity for improved frequency selectivity. Worst transient response with ringing.
- Elliptic: Most non-linear phase but sharpest frequency discrimination.
When rectangular pulses pass through these filters, Butterworth and Chebyshev filters will exhibit overshoot or ringing. If this is undesirable, Bessel filters (part of the Gaussian family) should be used to maintain linear phase.
Selectivity vs. Complexity
The component count required for equivalent performance varies significantly:
Component Requirements (from least to most for same specification):
- Chebyshev: Minimum components, steepest roll-off per component
- Elliptic: Slightly more components, but sharpest absolute roll-off
- Butterworth: Moderate component count, balanced performance
- Bessel: Maximum components, gentlest roll-off
This directly impacts:
- Circuit board space and layout complexity
- Cost of implementation
- Power consumption
- Potential failure points
Passband and Stopband Characteristics

Passband Ripple:
- Bessel & Butterworth: No ripple (monotonic decrease)
- Chebyshev Type I & Elliptic: Controlled ripple (adjustable parameter)
- Chebyshev Type II: No ripple (maximally flat)
Stopband Characteristics:
- Bessel & Butterworth: No ripple (all-pole configuration)
- Chebyshev Type I: No ripple
- Chebyshev Type II & Elliptic: Ripple present (includes zeros)
Attenuation in Transition Band (1kHz to 4kHz in typical comparison):
- Chebyshev: Highest attenuation (sharpest)
- Butterworth: Good moderate attenuation
- Bessel: Least attenuation (slowest)
Transient Response Comparison
The step response reveals how filters behave in the time domain:
Settling Time (for typical 0dB gain, -3dB at 1kHz, -40dB at 4kHz design):
- Bessel: ~1ms (fastest, minimal/no overshoot)
- Butterworth: ~3ms (moderate, single 10% overshoot)
- Chebyshev: ~7ms (slowest, significant ringing and overshoot)
Transient Response Quality:
- Best: Bessel - signal shape preserved with only delay
- Good: Butterworth - acceptable overshoot
- Worst: Chebyshev - significant ringing causes pulse distortion
Sensitivity to Component Tolerances
Real-world implementations must account for component variations from nominal values:
Tolerance Sensitivity (most to least forgiving):
- Bessel: Most forgiving, low sensitivity
- Butterworth: Forgiving, good tolerance to variations
- Chebyshev: More sensitive, may require tighter specifications
- Elliptic: Most sensitive, careful design and selection needed
This tolerance sensitivity affects manufacturing costs, as tighter component specifications increase expense.
Summary Comparison Table
| Characteristic | Butterworth | Bessel | Chebyshev | Elliptic |
|---|---|---|---|---|
| Passband Flatness | Maximally flat | Monotonic decrease | Ripple (Type I) | Ripple |
| Stopband Ripple | None | None | None (Type I) | Ripple |
| Roll-off Steepness | Moderate | Slowest | Steep | Steepest |
| Phase Linearity | Moderate | Best | Poor | Worst |
| Group Delay | Variable | Constant | Variable | Variable |
| Transient Settling | Moderate | Fastest | Slowest | Variable |
| Overshoot/Ringing | Some | Minimal | Significant | Significant |
| Component Count | Moderate | Highest | Lowest | Low-Moderate |
| Tolerance Sensitivity | Low | Low | Moderate | High |
| Best Use Case | General purpose | Time-domain critical | Frequency selection | Maximum selectivity |
Design Decision Framework
Choosing the right filter involves systematically evaluating your requirements:
Critical Questions to Ask:
- Is phase linearity critical?
- Yes → Bessel filter (only option for truly linear phase)
- Somewhat → Butterworth (reasonable compromise)
- No → Chebyshev or Elliptic (optimize for frequency response)
- How much frequency separation exists between passband and stopband?
- Generous separation → Bessel or Butterworth acceptable
- Limited separation → Chebyshev or Elliptic necessary
- Extremely tight → Elliptic (maximum performance per order)
- Can you tolerate passband ripple?
- No ripple tolerable → Butterworth or Chebyshev Type II
- Small ripple acceptable → Chebyshev Type I
- Willing to optimize ripple for performance → Elliptic
- What are the component count and complexity constraints?
- Minimize components → Chebyshev
- Cost-sensitive with good specs → Butterworth
- Performance over component count → Bessel or Elliptic
- Is this a general-purpose application?
- Unknown requirements → Butterworth (safe default choice)
- Well-defined specs → Choose based on critical parameters
- Multiple conflicting requirements → May need multiple filter stages
- What dominates: time-domain or frequency-domain performance?
- Time-domain (pulse, video, measurements) → Bessel
- Frequency-domain (channel separation, spectrum) → Chebyshev or Elliptic
- Both important → Butterworth compromise
Application-Specific Guidance
Audio Processing:
- General audio: Butterworth (flat response, acceptable phase)
- Critical listening: Bessel (preserves transients)
- Anti-aliasing/reconstruction: Chebyshev Type II or Elliptic
Communications Systems:
- Channel filtering: Chebyshev or Elliptic (tight spacing)
- Demodulator input: Consider bandwidth to manage phase issues
- Wide bandwidth: Butterworth sufficient
Measurement & Instrumentation:
- Waveform fidelity: Bessel mandatory
- Noise rejection: Butterworth or Chebyshev
- Spectral analysis: Any filter appropriate to requirements
Data Acquisition:
- Anti-aliasing: Bessel (minimal distortion) or Elliptic (sharp cutoff)
- Signal conditioning: Butterworth (general purpose)
Implementation Topologies

The filter type (Butterworth, Chebyshev, Bessel, or Elliptic) is independent of the circuit topology used to implement it. Common active filter topologies include:
Popular Active Filter Implementations:
- Sallen-Key Topology
- Low component count
- Good for low-order sections
- Unity or moderate gain
- Used for all classical filter types
- Multiple Feedback (MFB)
- Inverting configuration
- Good high-frequency performance
- Tight component tolerances
- Suitable for all filter types
- State Variable (Biquad) Filters
- Simultaneous LP, HP, BP outputs
- Independent adjustment of parameters
- More components but excellent control
- Can implement any filter type
Any of these topologies can realize Butterworth, Chebyshev, Bessel, or Elliptic responses. The choice of topology depends on:
- Available op-amp specifications
- Component tolerance requirements
- Frequency range of operation
- Desired gain configuration
- Number of required outputs
Digital Implementation Considerations
While analog filter theory provides the foundation, digital implementations through DSP or software offer distinct advantages and considerations.
Digital Filter Advantages:
Perfect Component Matching: Digital implementations eliminate tolerance issues entirely. Every coefficient is exact, ensuring the filter behaves exactly as designed.
Reconfigurability: Parameters can be changed in real-time through software, enabling adaptive filtering that’s impossible in analog circuits.
Reproducibility: Once designed, digital filters work identically across all implementations without calibration or component selection.
No Drift: Unlike analog components that age and drift with temperature, digital filters maintain constant performance over time and environmental conditions.
Digital-Specific Considerations:
Computational Cost: Different filter types have varying computational requirements:
- IIR filters (Butterworth, Chebyshev, Elliptic): Low computational cost, fewer operations
- FIR filters: Higher cost but guaranteed linear phase
- Higher-order filters: More multiply-accumulate operations
Quantization Effects: Finite precision in digital systems can cause:
- Coefficient quantization affecting frequency response
- Round-off noise accumulating through calculations
- Limit cycles in IIR implementations
Sample Rate Requirements: Digital filters must operate well above the Nyquist rate. Consider:
- Oversampling for better alias rejection
- Multirate techniques for computational efficiency
- Anti-aliasing filters before ADC
Hybrid Approaches:
FIR vs IIR Trade-off:
- FIR filters guarantee linear phase (like Bessel) but require more computation
- IIR filters (digital implementations of classical types) are computationally efficient
- Consider FIR for phase-critical applications despite computational cost
Adaptive Filtering: Modern systems can dynamically adjust filter characteristics based on signal conditions, combining benefits of multiple filter types.
Multirate Signal Processing:
- Decimation and interpolation techniques
- Efficient filtering at different sample rates
- Polyphase implementations reducing computation
Python and MATLAB Implementation:
Both platforms offer comprehensive filter design capabilities:
# Python SciPy example
from scipy import signal
import numpy as np
# Design a 5th-order Butterworth filter
b, a = signal.butter(5, 0.3, 'low')
# Design Chebyshev with 1dB ripple
b, a = signal.cheby1(5, 1, 0.3, 'low')
# Design Bessel for linear phase
b, a = signal.bessel(5, 0.3, 'low', norm='phase')
# Design Elliptic with passband and stopband specs
b, a = signal.ellip(5, 1, 40, 0.3, 'low')
These tools handle the mathematical complexity, allowing engineers to focus on specification and validation.
Practical Design Tools and Resources

Modern filter design leverages sophisticated software tools that eliminate manual calculations while providing visualization and analysis:
Software Tools:
MATLAB/Octave Signal Processing Toolboxes
- Comprehensive filter design functions
- Interactive Filter Design and Analysis Tool (fdatool)
- Automatic filter order estimation
- Frequency response visualization
- Group delay and phase analysis
- Zero-pole plots
- Time-domain simulation
Python SciPy
- Extensive
signalmodule for filter design - All classical filter types supported
- Integration with NumPy for numerical work
- Matplotlib for visualization
- Free and open-source
Analog Devices Filter Wizard
- Web-based, no installation required
- Immediate frequency response plots
- Component value calculation
- Export to SPICE formats
- Optimized for Analog Devices products
LTspice
- Free SPICE simulator from Analog Devices
- Accurate analog circuit simulation
- Verify theoretical designs with real components
- Transient and AC analysis
- Extensive component models
GNU Radio
- Open-source SDR framework
- Excellent for communications system filter design
- Visual programming with flowgraphs
- Real-time signal processing
Online Calculators
- Sallen-Key filter calculators
- Multi-feedback filter calculators
- Quick prototyping and component selection
Design Workflow:
- Specify Requirements: Define passband, stopband, ripple, attenuation
- Select Filter Type: Based on critical parameters (phase vs. frequency)
- Determine Order: Calculate minimum order meeting specifications
- Choose Topology: Sallen-Key, MFB, or State Variable
- Simulate: Verify performance in software (SPICE, MATLAB, Python)
- Prototype: Build and measure actual circuit
- Iterate: Refine based on measurements and real-world behavior
Advanced Topics and Considerations
All-Pole vs. Pole-Zero Configurations
An important distinction exists in filter architecture:
All-Pole Filters (Butterworth and Bessel):
- Transfer function contains only poles, no zeros
- Ensures no ripple in stopband
- Simpler mathematical description
- Generally easier to implement
Pole-Zero Filters (Chebyshev Type II and Elliptic):
- Include both poles and zeros in transfer function
- Zeros create transmission nulls (infinite attenuation at specific frequencies)
- Enable ripple trade-offs for steeper roll-off
- More complex but more flexible design space
Filter Order Determination
The required filter order depends on specification stringency. For equivalent attenuation performance:
- Elliptic: Lowest order (most efficient)
- Chebyshev: Low-moderate order
- Butterworth: Moderate-high order
- Bessel: Highest order (least efficient in frequency domain)
Example: To achieve 40dB attenuation at 4× cutoff frequency:
- Elliptic might need 3rd order
- Chebyshev needs 4th order
- Butterworth needs 5th order
- Bessel needs 7th order
Higher order means more stages, components, cost, and power consumption.
Cascading and Multi-Stage Designs
Complex specifications often require cascading multiple filter sections:
Series Cascading:
- First-order and second-order sections (biquads)
- Easier to implement and adjust
- Better dynamic range control
- Can mix filter types (e.g., Butterworth + Bessel)
Practical Considerations:
- Op-amp noise contributions accumulate
- Inter-stage impedance matching required
- Total phase shift is sum of individual stages
- Group delay is additive
Temperature and Aging Effects
Analog implementations face long-term stability challenges:
Temperature Coefficients:
- Resistors: ±25 to ±100 ppm/°C typical
- Capacitors: Can vary widely by type
- Op-amp parameters shift with temperature
- Affects both cutoff frequency and Q factor
Aging and Drift:
- Capacitor values change over years
- Resistance drift, especially in thin-film types
- Filter performance degrades gradually
- Periodic recalibration may be needed
Digital filters eliminate these concerns entirely.
Power Consumption and Noise
Analog Filter Considerations:
- Each op-amp consumes quiescent current
- Higher-order filters need more stages
- Voltage noise from op-amps and resistors
- Current noise from active devices
- Trade-off between noise and power
Digital Filter Considerations:
- Power scales with sample rate and complexity
- Can use low-power modes when inactive
- Quantization noise vs. bit depth
- Can implement sophisticated noise shaping
Real-World Design Example
Let’s walk through a practical design scenario:
Specification: Anti-aliasing filter for a 20kHz audio ADC
Requirements:
- Passband: DC to 18kHz (flat response desired)
- Stopband: >22kHz with >60dB attenuation
- Minimal phase distortion in audio range
- Low component count for cost
Analysis:
- Bessel: Excellent phase, but requires high order (expensive, excessive attenuation of high frequencies)
- Butterworth: Good compromise - flat passband, moderate phase, reasonable order (~6th order needed)
- Chebyshev: Lower order (~4th), but passband ripple affects audio quality
- Elliptic: Lowest order (~3rd), but both ripple and poor phase unacceptable for audio
Decision: 6th-order Butterworth
- Provides needed attenuation (120dB/decade)
- Maximally flat in audio band
- Acceptable phase response
- Reasonable component count (3 biquad sections)
Implementation: Three cascaded Sallen-Key biquads with calculated component values, followed by validation in LTspice.
This example demonstrates the systematic approach: define specs, evaluate each filter type against requirements, make informed trade-off decisions.
Conclusion
The journey through filter topologies reveals that there is no universally “best” filter - the optimal choice depends entirely on your application’s requirements and constraints. Each of the four classical approximations offers distinct advantages:
Bessel filters sacrifice frequency selectivity for unmatched time-domain performance. Choose them when signal shape, timing, and phase linearity are paramount - when preserving the input waveform matters more than sharp frequency discrimination.
Butterworth filters represent the golden mean, offering flat passband response and reasonable roll-off without ripple complications. Their forgiving nature and general-purpose characteristics make them the default choice for many applications.
Chebyshev filters push frequency selectivity to new levels, accepting passband or stopband ripple as the price for steeper roll-offs with fewer components. They’re workhorses in communications and RF systems where spectrum is precious.
Elliptic filters achieve maximum frequency selectivity, providing the sharpest possible transition between passband and stopband by allowing ripple in both regions. When adjacent channel rejection or tight frequency spacing dominates all other concerns, elliptic filters deliver unmatched performance.
Understanding these fundamental characteristics and trade-offs empowers engineers to make informed decisions that balance performance, complexity, and cost. The art of filter design lies not just in knowing these options exist, but in deeply understanding which trade-offs matter most for your specific use case.
Modern tools like MATLAB, Python SciPy, and specialized filter calculators have democratized filter design, eliminating much of the mathematical tedium. Yet the conceptual understanding remains crucial - tools can calculate component values, but only human engineers can determine whether phase linearity trumps roll-off steepness, whether 1dB of ripple is acceptable, or whether the application demands the simplicity of Butterworth or the performance of Elliptic.
As signal processing continues evolving, with hybrid analog-digital systems, adaptive filtering, and software-defined approaches, these classical filter types remain foundational. Whether implemented in discrete components, integrated circuits, or digital signal processors, the fundamental trade-offs between Bessel, Butterworth, Chebyshev, and Elliptic filters continue to shape how we filter, condition, and process signals in virtually every electronic system.
The next time you design a filter, remember: the choice isn’t about finding the “best” filter type - it’s about finding the right filter for your application’s unique balance of requirements.
References and Further Reading
Primary Sources:
- Butterworth, S. (1930). “On the Theory of Filter Amplifiers,” Wireless Engineer, 7:536-541
- Original article: Filter Topology Face-Off by Bliley Technologies
- Butterworth and Chebyshev Filters - Analog Circuit Design
Recommended Resources:
- Williams, A.B. and Taylor, F.J. “Electronic Filter Design Handbook” - Comprehensive reference
- Schaumann, R. and Van Valkenburg, M.E. “Design of Analog Filters” - Detailed theory and design
- Oppenheim, A.V. and Schafer, R.W. “Discrete-Time Signal Processing” - Digital implementation
- Application notes from Analog Devices, Texas Instruments, and Linear Technology
- IEEE Transactions on Circuit Theory - Historical papers on filter design
Online Resources:
- MATLAB Filter Design Toolbox documentation
- SciPy Signal Processing documentation
- Analog Devices Engineer Zone
- All About Circuits filter design tutorials
Have questions about filter design or want to share your experiences with different filter topologies? Feel free to reach out or leave comments below.
